What is linear and binary search? : Implementation, Difference, and More
- Pushp Raj
- Apr 13, 2023
- 8 min read

Searching a data structure refers to finding a desired element in a set of elements. The desired item is called a "target". The set of items to search can be any data structure, such as A list, array, linked list, tree, or chart.
Searching Methods
Searching in the data structure can be done by applying searching algorithms to check for or extract an element from any form of stored data structure.
These algorithms are classified according to the type of search operation they perform, such as:
Sequential search
The list or array of elements is traversed sequentially while checking every component of the set.
For example – Linear Search.
Interval Search
The interval search includes algorithms that are explicitly designed for searching in sorted data structures. In terms of efficiency, these algorithms are far better than linear search algorithms.
Example- Logarithmic Search, Binary search.
These search algorithms can be used to solve various problems related to DSA, such as: B. Finding a specific element in an array or linked list, reordering elements in an array or linked list, and so on.
What is Linear Search?
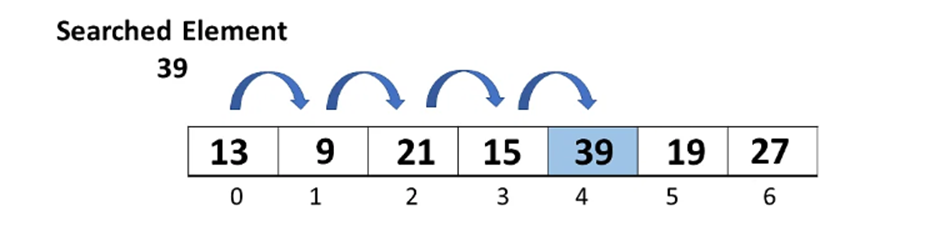
A linear search is also called a sequential search algorithm. The simplest search algorithm. A linear search traverses the list completely, matching each element with the element at the position you want to search. If a match is found, the item's location is returned. Otherwise, the algorithm returns NULL.
It is often used to find elements from unordered lists. H. A list whose elements are unsorted. The worst-case time complexity of the linear search is O(n).
How to implement Linear Search Algorithms?
Following is a step-by-step approach employed to implement Linear Search Algorithm.
Step 1: First, read the search element (Target element) in the array.
Step 2: In the second step compare the search element with the first element in the array.
Step 3: If both are matched, display "Target element is found" and terminate the Linear Search function.
Step 4: If both are not matched, compare the search element with the next element in the array.
Step 5: In this step, repeat steps 3 and 4 until the search (Target) element is compared with the last element of the array.
Step 6: If the last element in the list does not match, the Linear Search Function will be terminated, and the message "Element is not found" will be displayed.
So far, you have explored the fundamental definition and the working terminology of the Linear Search Algorithm.
Code Sample -
#include <iostream>
using namespace std;
int search (int array[], int n, int x) {
// Going through array sequencially
for (int i = 0; i < n; i++)
if (array[i] == x)
return i;
return -1;
}
int main() {
int array[] = {2, 4, 0, 1, 9};
int x = 1;
int n = sizeof(array) / sizeof(array[0]);
int result = search(array, n, x);
(result == -1) ? cout << "Element not found" : cout << "Element found at index: " << result;
}
Time complexity analysis
Best case:
The best case is when the target element is the first element of the array. In this case, the number of comparisons is 1, so the time complexity is O(1).
Average case:
On average, the target element is somewhere in the middle of the array. In this case, the number of comparisons is N/2. So the time complexity is O(N) (ignoring constants).
Worst case:
The worst case happens when the target element is the last element of the array or is not in the array. In this case, the number of comparisons is N because we need to iterate over the array. So, the time complexity is O(N).
Space Complexity:
Since linear search uses no extra space, its space complexity is O(n), where n is the number of elements in an array.
Application of Linear Search Algorithm
The linear search algorithm has the following applications:
· Linear search can be applied to both single-dimensional and multi-dimensional arrays.
· Linear search is easy to implement and effective when the array contains only a few elements.
· Linear Search is also efficient when the search is performed to fetch a single search in an unordered-List.
Advantages of Linear Search
· Easy to understand
· No special data structure is
· Can be used with unsorted data
· No additional memory
· Independent of data size
Disadvantages of Linear Search
· Time-consuming
· Not suitable for large amounts of data
· Not suitable for ordered
· Not suitable for repetitive tasks
· Not suitable for real-time
What is Binary Search?
Binary search is an efficient algorithm based on the concept of "divide and conquer", performing a search by recursively splitting the array in half until an element is found or the list is narrowed down to the part that does not match the required item. improve.
Binary search works on the principle of using sorted information in an array to reduce the time complexity to zero (log n).
Approach for binary search:
Step 1: Compare the target element with the middle element of the array.
Step 2: If the target element is greater than the middle element, then the search continues in the right half.
Step 3: Else if the target element is less than the middle value, the search continues in the left half.
Step 4: This process is repeated until the middle element is equal to the target element, or the target element is not in the array
Step 5: If the target element is found, its index is returned, else -1 is returned.
Key Point - middle = initial_value + end_value / 2 ;
How to implement binary search?
There are two forms of binary search implementations:
· Iterative
· Recursive methods.
The most important difference between the two methods is that the recursive method has a spatial complexity of O(logN) while the iterative method uses O(1). The recursive version is easier to implement, but the iterative approach is more efficient.
An iterative algorithm repeats a specified set of instructions a specified number of times. This algorithm repeats the same steps multiple times using loop statements (loops, while loops, do-while loops, etc.). A recursive algorithm, on the other hand, relies on a function calling itself repeatedly until a basic condition (also called a stopping condition) is reached.
What is an iterative algorithm?
An iterative algorithm repeats a specific set of instructions a specific number of times. Iterative algorithms use looping statements such as for loops, while loops or do-while loops to repeat the same procedure multiple times.
Sample Code in C++ -
#include <iostream>
using namespace std;
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int x = 4;
int n = sizeof(array) / sizeof(array[0]);
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}
What is a Recursive Algorithm?
In a recursive algorithm, a function keeps calling itself until a basic condition (the stopping condition) is met.
Let us traverse the search space by starting and ending two indexes. Initially low = 0, high = n-1 (initially the entire array is the search space). At each step, find the mean in your search space and compare it to the target value. There are three possible cases:
Case 1: Returns the center if the target is equal to the center.
Case 2: If the target is less than the middle i.e., target<A[mid], we discard all the elements in the right search space including the mid element. Now our new high would be mid-1 while the `low` remains as it is.
Case 3: If the target element is greater than the middle i.e., target>A[mid], we discard all the elements in the left search space including the mid element. Now our new low would be mid+1 while the 'high' remains as it is.
Sample Code in C++ -
#include <iostream>
using namespace std;
int binarySearch(int array[], int x, int low, int high) {
if (high >= low) {
int mid = low + (high - low) / 2;
// If found at mid, then return it
if (array[mid] == x)
return mid;
// Search the left half
if (array[mid] > x)
return binarySearch(array, x, low, mid - 1);
// Search the right half
return binarySearch(array, x, mid + 1, high);
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int x = 4;
int n = sizeof(array) / sizeof(array[0]);
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}
Time Complexity
Best Case – The best case occurs when the element to search is found in the first comparison, i.e., when the first middle element itself is the element to be searched. The best-case time complexity of Binary search is O(1).
Average Case - The average case time complexity of the binary search is O(logn).
Worst-Case – Binary search has the worst case when the search space needs to be further reduced to have only one element. Worst-case binary search has O(logn) time complexity.
Run-time complexity - O (log n)
Space complexity is O(1).
Binary search using Iterative and recursive method: Binary Search Implementation
When to use a binary search?
It is much faster than linear search because it has O (log n) time complexity when searching large datasets.
· If the records are sorted.
· If the data is stored in contiguous memory.
· Data does not have complex structures or relationships.
Applications of Binary Search
· This algorithm is used to search elements in each sorted array with more efficiency.
· It could also be used for a few other additional operations like- finding the smallest element in the array or finding the largest element in the array.
Real-world Application
· Dictionary
· Debugging a linear piece of code
· Figuring out resource requirements for a large system
· Find values in a sorted collection
· Semiconductor test programs
· Numerical solutions to an equation
Advantages of binary search
· Binary search is faster than linear search, especially for large arrays. As the array size increases, the time it takes to perform a linear search increase linearly, while the time it takes to perform a binary search increase logarithmically.
· Binary search is more efficient than other search algorithms with similar time complexity. Interpolation search or exponential search.
· Binary search is relatively simple to implement and easy to understand, making it suitable for many applications.
· Binary search can be used on both sorted arrays and sorted linked lists, making it a flexible algorithm. Binary search is suitable for searching large datasets stored in external storage, such as B. Hard Drive or Cloud.
· Binary search can be used as a building block for more complex algorithms, such as those used in computer graphics and machine learning.
Drawbacks of binary search
· If the array is not sorted, it must be sorted first before doing the search. This adds
O(nlog n) time complexity to the sorting step and can make binary searches less
efficient for very small arrays.
· Binary search requires that the array to be searched be stored in contiguous locations. This can be a problem if the array is too large to fit in memory, or if the array is stored on external storage such as a hard drive or cloud.
· Binary search requires that the array elements are comparable. That is, you can sort them. This can be a problem if the elements of the array are not naturally ordered, or if the order is not well defined.
· Binary search can be less efficient than other algorithms such as B. Hash tables for searching very large data sets that do not fit in memory.
Read, Also - Graph in DSA: Definition, Types, Applications & More



Comments